数理論 へ戻る（１） 細胞分裂のモデル
-
藻類は細胞分裂により増殖していきます。 その増殖の仕方には次のような法則があるものが多いとのことです。
細胞分裂するのは「 青年細胞 」が成長した「 熟年細胞 」ですが、「 熟年細胞 」は「 青年細胞 」と「 少年細胞 」とに分裂します。「 少年細胞 」は、 自分と一緒に生まれた「 青年細胞 」が「 熟年細胞 」になって分裂する頃に「 青年細胞 」へと成長し、 自分と一緒に生まれた「 青年細胞 の「 初孫細胞 」が誕生する頃に「 熟年細胞 」になって分裂します。
「 青年細胞 」を
、「 少年細胞 」を 
として、 以上の増殖の仕方を表にすると次のようになります。|
時刻 ０ 時 |
ａ |
１個 |
|
時刻 ｔ 時 |
Ａ |
１個 |
|
時刻 ２ｔ 時 |
Ａ ａ |
２個 |
|
時刻 ３ｔ 時 |
Ａ ａ Ａ |
３個 |
|
時刻 ４ｔ 時 |
Ａ ａ Ａ Ａ ａ |
５個 |
|
時刻 ５ｔ 時 |
Ａ ａ Ａ Ａ ａ Ａ ａ Ａ |
８個 |
|
時刻 ６ｔ 時 |
Ａ ａ Ａ Ａ ａ Ａ ａ Ａ Ａ ａ Ａ Ａ ａ |
13個 |
ではここで問題です。時刻
時には、細胞数は何個になるでしょうか？ の増え方 ： ０ １ １ ２ ３ ５ ８ の増え方 ： １ ０ １ １ ２ ３ ５―――――――――――――――――――――――――――――――――――
合 計 ： １ １ ２ ３ ５ ８ 13
合計の３項目以降は、 前の項と２つ前の項とを足したものになっています。 そこで
項目の値を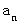 
として漸化式を作ると、 次のようになります。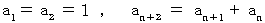
これはフィボナッチ数列です。 したがって、 答えはフィボナッチ数列の
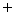
項目の値です。 その求め方については、 数理論 ＞ フィボナッチ数列 をご覧ください。-
ｎ 段の階段を２つ以上飛ばさずに上る場合の数を考えましょう。 １段の階段を上がるのは １通りあり、 ２段の階段を上がるのは２通りあります。 では、 ３段の階段について考えてください。
これも簡単ですね。 答えは、 １-２-３ と １-３ と ２-３ の ３通りです。 しかし、 別解答を考えてください。
３段の階段を上がる方法には、 ゴールの直前が２段目の場合と１段目の場合との２通りあります。 ゴールの直前が２段目の場合、 それ以前の場合の数は「 ２段の階段を上がる場合の数 」です。 ゴールの直前が１段目の場合は、 それ以前の場合の数は 「 １段の階段を上がる場合の数 」 です。 したがって、 ３段の階段を上がる場合の数は、 ゴールの直前が２段目の場合の数 と ゴールの直前が１段目の場合の数 とを加えて、 ３通りになります。
階段が４段以上の場合もこれと同様な考え方で答えを求めることができますので、 答えを ｎ ＝ １， ２， ３， ・ ・ ・ の順に並べていきますと、 准フィボナッツ数列 （ 初項を除いて第２項から始まるフボナッチ数列 ） になります。
-
６個碁石を一列に並べる場合を考えましょう。 ただし、 黒石が決して隣り合わないことを条件とします。
この条件に従ってｎ個の碁石を一列に並べる全ての場合の数を Ｐｎ 通り とします。
最後に並べるｎ個目の石が白石の場合 ：
Ｐｎ ＝ Ｐｎ−１
最後に並べるｎ個目の石が黒石の場合 ：
Ｐｎ ＝ Ｐｎ−２
したがって、
Ｐｎ ＝ Ｐｎ−１ ＋ Ｐｎ−２
Ｐ１ ＝ ２ Ｐ２ ＝ ３
よって、 Ｐ３ ＝ ５ Ｐ４ ＝ ８ Ｐ5 ＝ 13 Ｐ6 ＝ 21
したがって、 答えは 21 通り です。
十進BASIC ＞ 十進BASIC＿算数 ＞ 准フィボナッチ数列-
次の論文の中にもフィボナッチ数列の例があります。
数理論 ＞ ウサギ２進数列
十進BASIC ＞ 十進BASIC＿プログラミング ＞ 漸化式の作り方